There are many puzzles about the number squares you can draw by using the grid points ( lattice points) on a given grid. Here is an example;
The correct answer is not 9 (the number of 1x1 squares). There are many other squares you can create using the given points.

These hard to catch tilted squares makes these puzzles interesting!
Now we have a harder puzzle to work on!
What is the total number of squares that can fit into an n x n grid?
*Lattice squares are the squares whose vertices are on the grid points.
There are two types of lattice squares, grid ones and the tilted ones.
Let’s define a "grid square" as a square whose vertices are lattice points and sides are along the axis. (vertical squares). They are easy to create and have square number areas.

A "tilted square" is a square whose vertices are still lattice points, but its sides are not along the axis.

Tilted squares have whole number areas. The side length of a tilted square can easily be found by using the Pythagorean Theorem.

Now, let’s have a look at a 3 x 3 squares and find the total number of grid and tilted squares that can be drawn using the lattice points.

The number of grid squares that can be drawn is 9 +4 +1 = 14
Now, let’s find the number of tilted squares
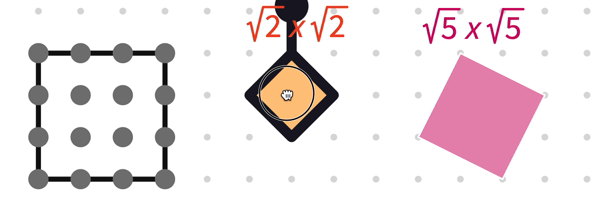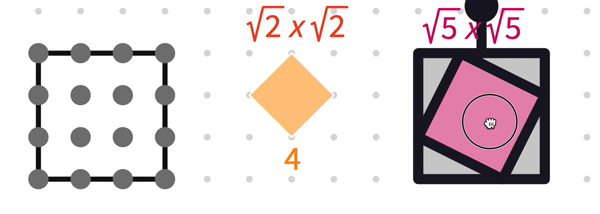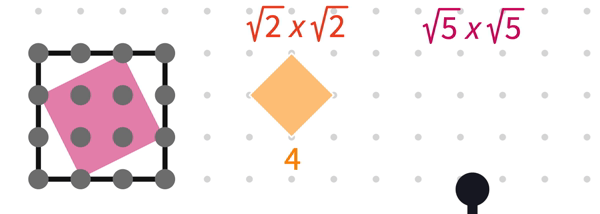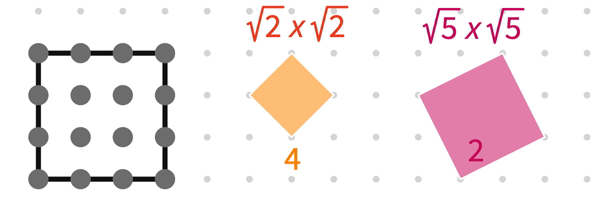
The number of tilted squares that can be drawn is 4 + 2 = 6.

Then, the total number of lattice squares is 14 + 6 = 20 by using the points of a 3 x 3 grid.
One may wonder if there is a short way of finding the number of squares for an n x n square.
The questions we need to answer are;
The number of grid squares in a n x n square
The side length of the biggest tilted square that can be drawn in an n x n square
The number of tilted squares in a n x n square
The total number of lattice squares in an n x n square.
Any relation among the number of tilted squares and grid squares
We need to investigate all the possible squares carefully and record our findings systematically to be able to find answers to these questions.
Here is a Polypad file you can work on to make drawings;
You may need more grids to highlight to create different squares. Good luck!
------ ***------
SOLUTION
We can start solving this puzzle by remembering another one! Famous" Checkerboard Puzzle".
The answer of the Checkerboard Problem gives us the number of grid squares.
To be able to find the total number of squares on a checkerboard, we need to consider that the board has 2 x 2 squares, 3 x 3 squares, 4 x 4 squares and so on other than 64 unit squares.
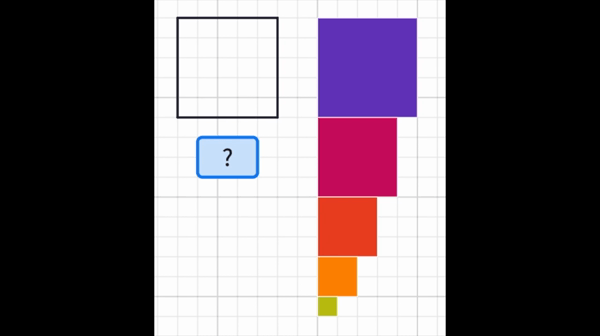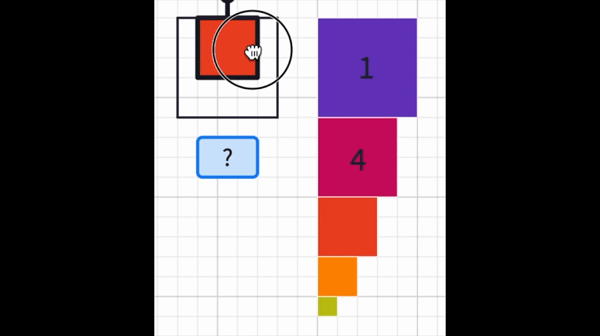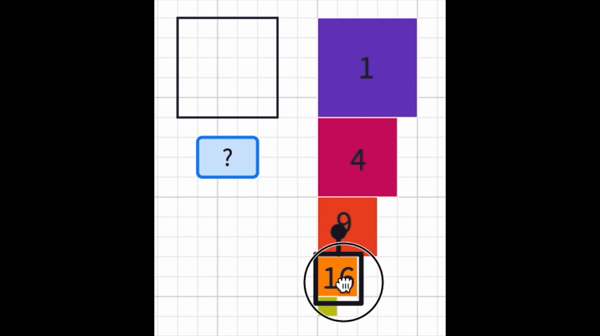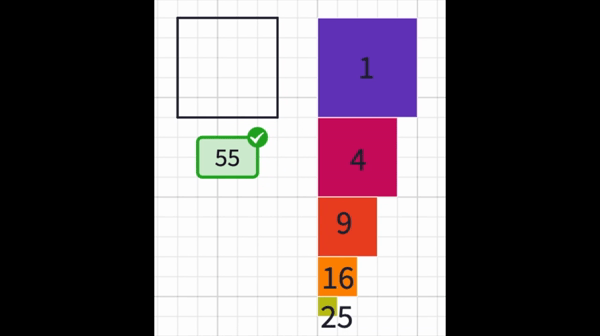
If we organize our findings in a table. We may easily see that they follow the pattern of square numbers.
Number of Grid squares in a n x n square;

So for an n x n grid, the number of normal grid squares is simply the sum of the square numbers.
One way to express the number of grid squares in an n x n grid is;

When it comes to find the number of the tilted squares, we may discover different patterns. If you need an extra help for finding the side lengths of the tilted squares, you may have a look at the Square Areas on Grid Polypad Activity.
When we organize the data for the tilted squares, one particular pattern can catch your eye. The number of √2 x √2 squares also follows the pattern of square numbers and so does 2√2 x 2√2 and 3√2 x 3√2 …

The other tilted squares with the side lengths √5, √10, √13 … can be tricky to count. Be aware the symmetry of the square can make a different square now!
√5 x √5 Example in a 4 x 4 grid square;

There are 8 of them. If we have a closer look to 4 x 4 grid square, we see that there are 20 tilted square and 30 grid squares.

Now, let’s have a look at the 5x5 case;

Now there are 50 tilted squares and 55 grid squares. If you repeat the same steps for a 6 x 6 grid;

We see that there are 105 tilted squares. You may realize that;
In a n x n grid, the total number of grid squares and tilted squares, is equal to the number of tilted squares in a (n+1)×(n+1) grid.

Now, let’s try to figure out the side length of the biggest tilted square that can fit into an n x n grid.
Let “c” be the side length of the tilted square in a grid. By Pythagorean theorem a^2+b^2=c^2 and we also know that a+b can be at most n units long.
a+b <= n

For example in a 5 x 5 grid; you may draw

“a+b” can never exceed the value of n.
Let’s now try to write the side lengths of the tilted squares which will be added to the list for an 7x 7 grid.
Find a + b <=7 the new values will be
6 +1 , 5+2 and 4+3

Now, let’s organize our findings about the tilted squares for each n x n grid;

Here you may want to double check your results by comparing the patterns you have discovered before.
Try to write the new values for 7x7

One way to express the number of tilted squares in a n x n square

So the total number of lattice squares in a n x n grid can be found by

These expressions can also prove our previous discovery about the total number of lattice squares in a n x n grid, the number of tilted squares in a (n+1)×(n+1) grid.
One of the best outcomes of working on a problem like this is the beauty of the solution!
Extension:
Can we derive a formula for the total number of lattice squares in an n x m rectangular grid where n>m?




